Ch6
Ch6
3
设
是恰有 个奇度顶点的连通图,证明: 中存在 条边不重的行迹 ,使得 。
将图
对每个子图来说,根据推论6.1,子图均存在2个奇度顶点,所以子图均有
4
如何将16个二进制数字(8个0,8个1)拍成一个圆形,使得16个长为4的二进制数在其中都出现且只出现一次。
转化成图论问题。
定义顶点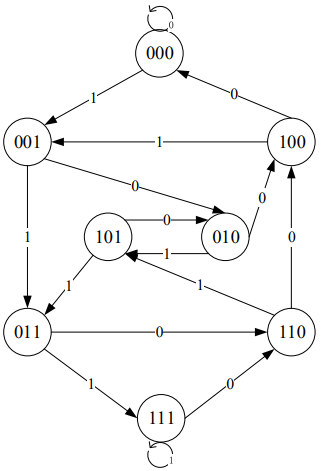
每个3位二进制数向左移位,可在其最右补0或1,则每个顶点
由
根据其中一条
8
求图6.28的一条最优投递路线。
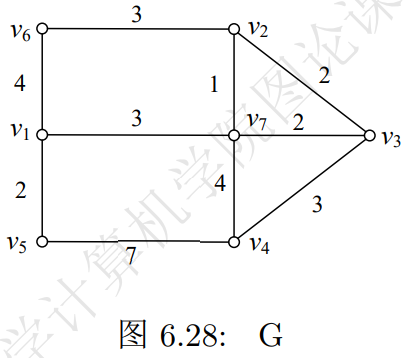
使用EJ算法。
(1)图
(2)由
(3)构成带权完成图
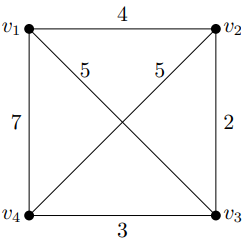
(4)上图
在
(5)
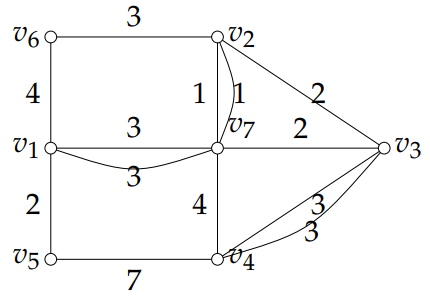
(6)在图
不妨设出发点(邮局)为
9
设
是二分图,证明:若 是 ,则 必有偶数个顶点。习题1中的图6.27是 图吗?为什么?
证明:设二分图
同理
在图6.27中,