Ch5

1*

分别求出和中不同完美匹配的个数。

的完备匹配个数等于将个元素划分成个大小为2的集合，个数为

的完备匹配可以对第一部分标号，第二部分与第一部分的匹配可以看成全排列，个数为.

2*

树至多有一个完备匹配

证明：
假设存在两个完备匹配和，设，与的顶点集合相同，任取一个顶点，在与中各有一个与其相连的边，设这两条边的另一个顶点为. 在中有一条与相连的边，在中有一条与相连的边，若这两条边的另一个顶点相同，设这个顶点为，则为圈，与树中无圈矛盾。若这两条边的顶点不同，设为，以此类推，必然会出现顶点相同的情况，为圈，与树中无圈矛盾。
故树之多有一个完备匹配。

7*

证明：二分图有完备匹配的充要条件是，对任意，都有。这个条件对一般图是否成立？

证明：
设,
则.
（必要性）：
因为二分图有完备匹配，所以中的顶点都被许配。
由定理，有. 同理，.

（充分性）：
不妨设，取，由定理，存在匹配，使得中的顶点都被匹配。

中的顶点也相应地都被匹配。所以匹配即为二分图的完备匹配。
对一般图不成立，例如满足，但是没有完备匹配。

13*

用定理来证明定理。

定理：图（G为一般图，不一定是二分图）由完备匹配，都有.
定理：二分图，且，存在将中的顶点都许配的匹配都有，其中为的邻顶集合。
证明：
对二分图，当为偶数时，加一些边使得为完全图；当时奇数时，加一些边和顶点使得是完全图。图变成完全图，中存在将中所有顶点都许配的匹配的充要条件是有完备匹配。此时定理等价于有完备匹配的充要条件是.
（必要性）：
, 由定理，
在中，中点都是孤立点，所以
.
（充分性）：
对，并设，且.
因为是一个完全图，则在中删去不会增加连通片个数，且最多产生一个奇片. 删去可能会使得中有孤立顶点，设此时中的孤立顶点为，则，则有
若，则；
若，则；
若为偶数，则；
若为奇数，则；
综上，对，都有. 由定理，为有完备匹配的图。

14

证明：树有完备匹配，当且仅当对任意，都有。

证明：
（必要性）：
树T有完备匹配，由定理，, 都有.
令，则.
由于树T由完备匹配，即为偶数，则为奇数。
.
综上，.
（充分性）：
，都有，则为偶数。
删去后，树被划分成若干个连通片，且只有一个连通片为奇片，设奇片中与相连的顶点为，在树中，确定一个后，由于，所以被唯一确定。
被唯一确定。
是任意的
所有相对应的的集合就是T的完备匹配。
综上，树具有完备匹配。

17

设有四个人，有四分工作，每个人做某份工作的效率如下面的矩阵所示，试求最佳的工作分配方案

按照算法一步步计算即可。
构造相等子图

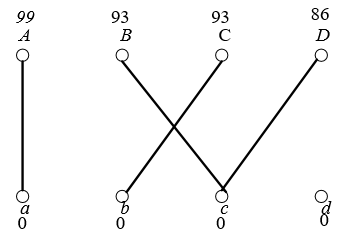
无完备匹配，取D为未被许配的点，可得：



，重新构造相等子图：

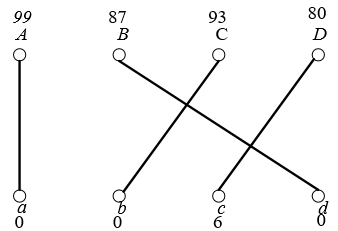
最佳分配方案为：.

19

证明：算法中修改顶标后，仍然是可行顶标。

证明：
修改的可行顶标

对,
(1) 若，则.
(2) 若，
，
.
对,
.
综上，算法修改顶标后，仍然是可行顶标。