Ch2

、

2*

一棵树T有 个 度数为 的顶点， , 其余顶点都是树叶，则T有几片树叶？

由图的性质有：

由树的性质有：

上面两个式子联立可得：

4*

证明：如果T是树，且 ，则T至少有n片树叶

由2.2题的结论我可以可以得到：

得证

6*

证明：树有一个中心或两个中心，且有两个中心时，这两个中心相邻

方法一

可以使用删除叶子节点的方法，即证明删除中所有叶子结点后，新树的中心不变。

对于 ，如果要使最大，v显然是叶子。那么删除所有 中叶子结点后，必然有：

所以u仍为的中心。

重复执行上述操作，最后只能得到这两种情况，即一个顶点或者两个相邻顶点，得证。

方法二

可以用最长轨法证明最长轨的中点为树的中心。

11*

求 生成树的个数

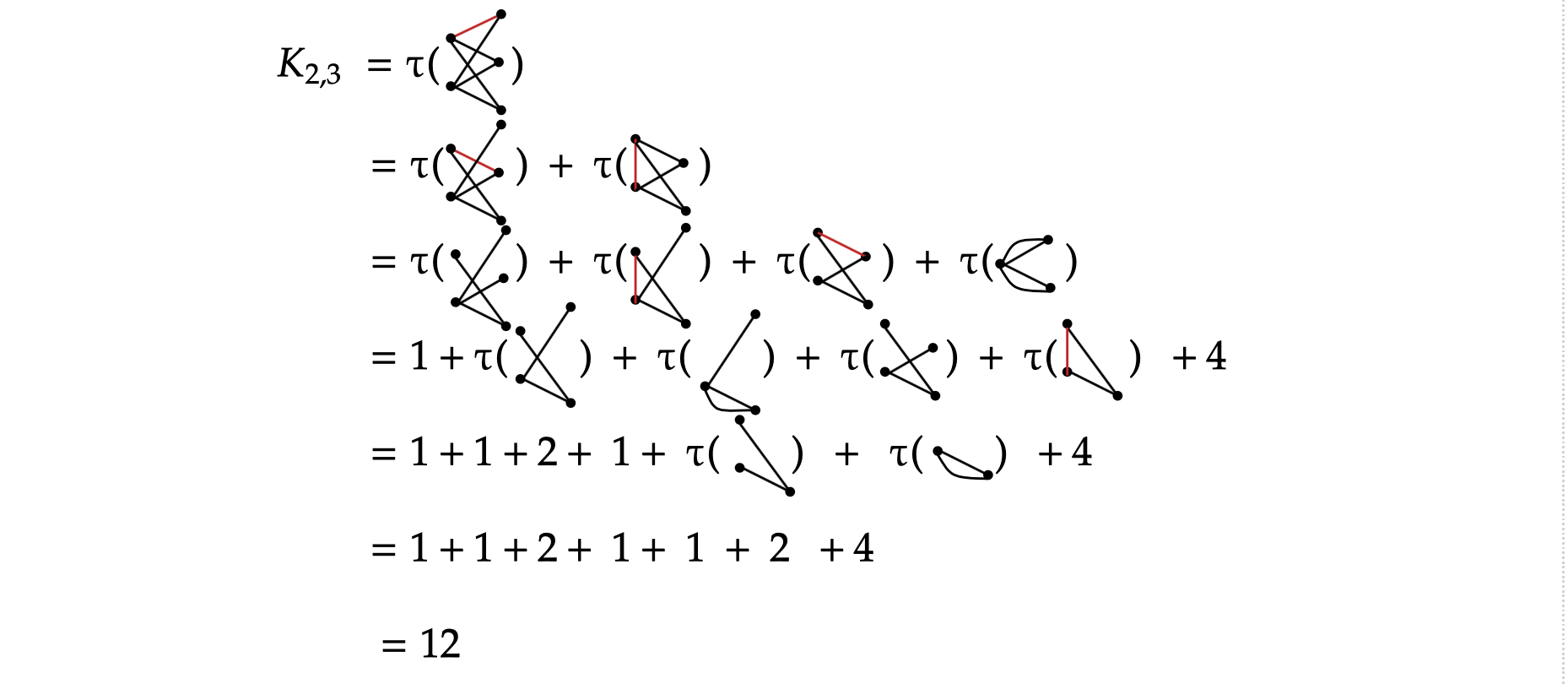
14*

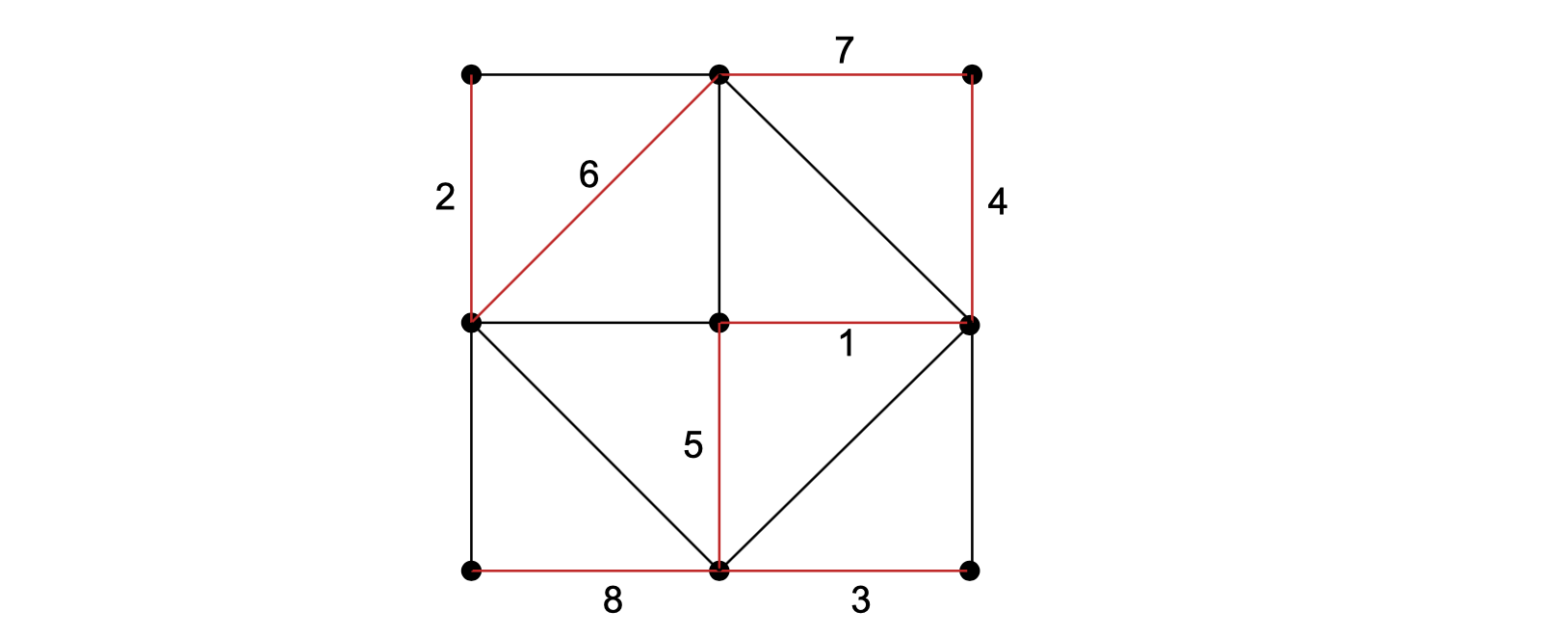
用Kruskal算法求图中边权图最小的生成树

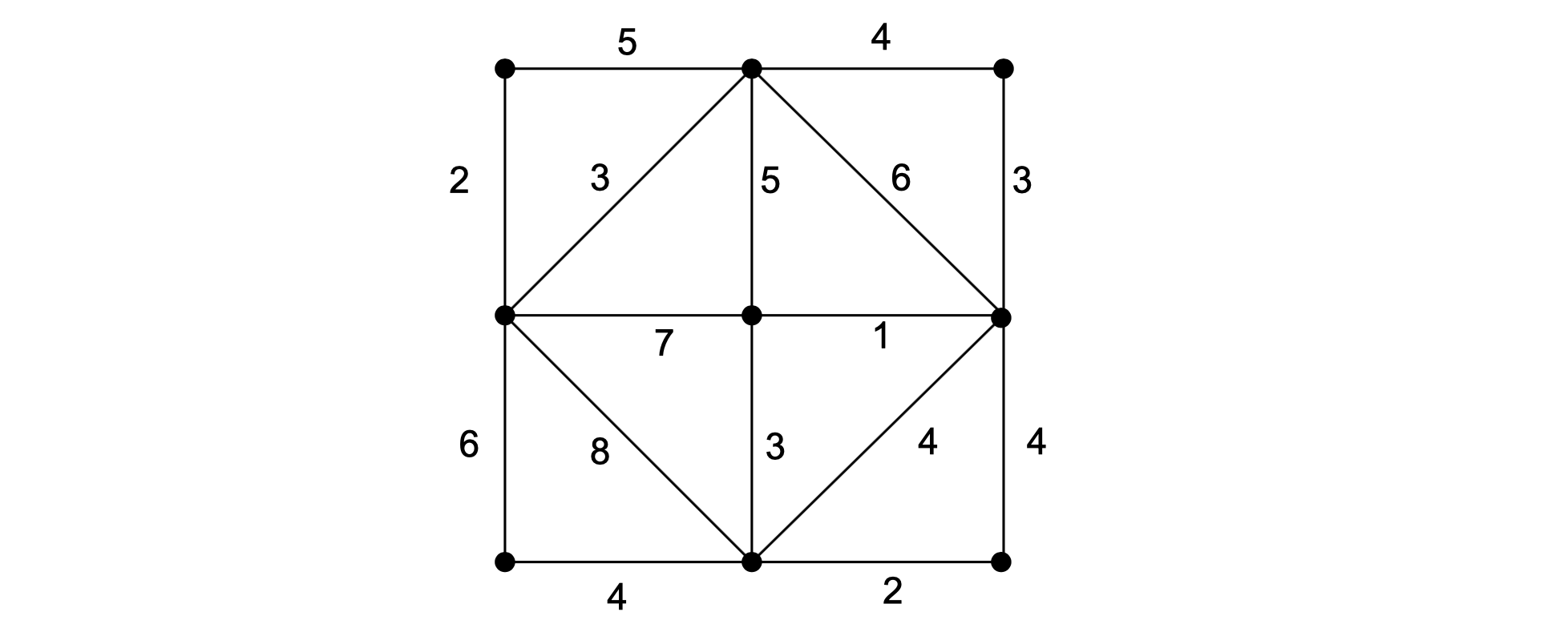
Kruskal的算法是有限选择边权较小的边，选择的顺序是和Prim算法不一样的是，如下图所示，红色标记的是最小生成树，序号则是顺序。

15*

边权图里的最小生成森林是权最小的生成森林，并且在生成森林中 保持原图中任意两个顶点的连通性。如何修改 Kruskal 算法来构造最小 生成森林，并指出时间复杂度。

**Kruskal算法 ** ：

• 输入：加权图
• 输出：G的一棵生成树的边子集

过程如下：

1. 从E中选权最小的边;
2. 若已经选定边，则从中选取边，使得
   • (i)边导出子图不含圈；
   • (ii)在满足(i)的前提下，的权最小，即
3. 反复执行第(2)步，直到选出为止

下面分类讨论：

1. 如果知道G的连通片数，设为k

   则在各连通片上分别执行原Kruskal算法，时间复杂度为：

2. 如果不知道G的连通片数， 则需修改循环中止条件：

   改为反复执行第(2)步，直到从剩余边集中选出任意一条边都会使边导出子图含圈

   时间复杂度为

20*

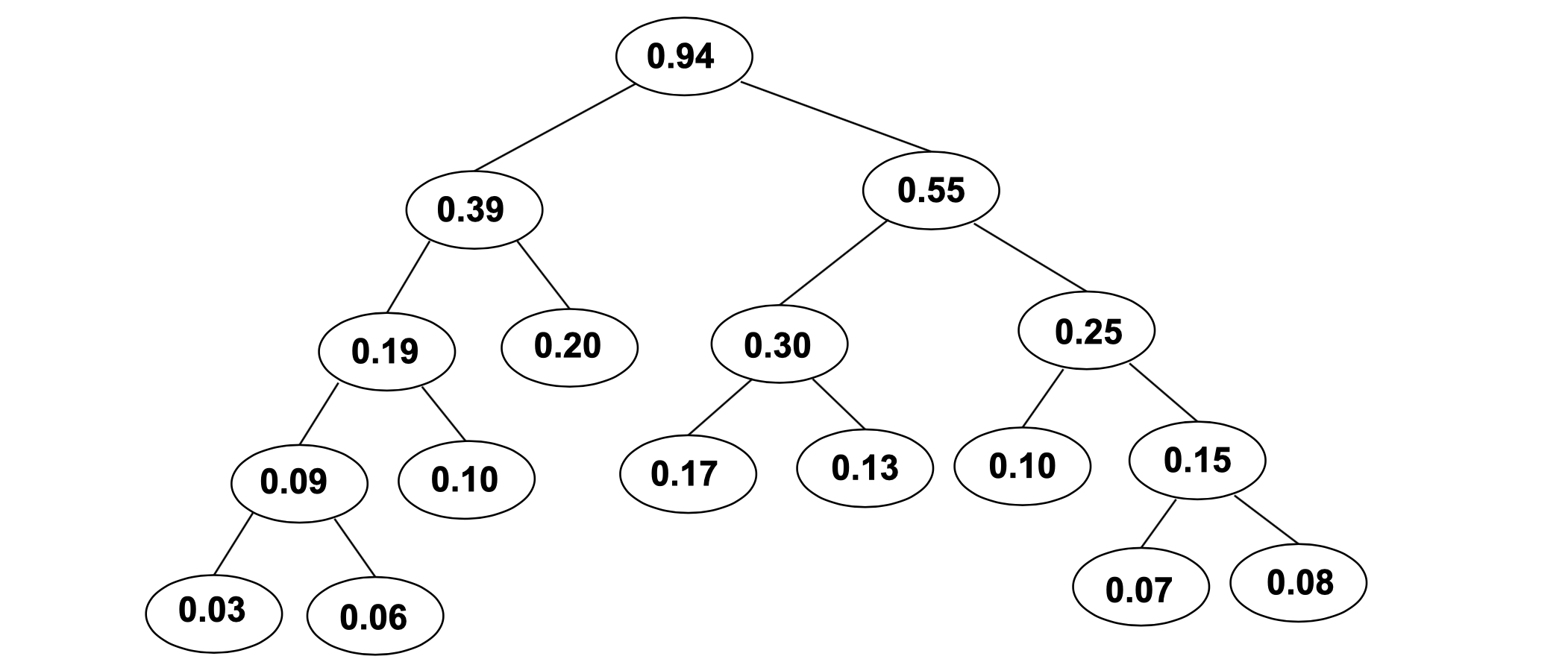
画出带权 0.2,0.17,0.13,0.1,0.1,0.08,0.06,0.07,0.03 的 Huffman 树

需要注意的是此题的权重之和并不是1，许多人误以为权重之和必须是1。

22*

证明引理2.1

给定，则存在一课Huffman树，使得对应的顶点时兄弟，且这两个顶点在二叉树中的深度都等于树高

不妨设对应的顶点为，假设任意Huffman树中中的深度不等于树高，即存在，使得的深度大于树高 ，显然有。

因为

且

交换的位置，得到 ，则有

1. 当时，，与树同为Huffman树；
2. 当时，，与树为Huffman矛盾；

则的深度等于树高，且同理可证得

若无兄弟，则由Huffman树WPL最小规则，得深度还可以再缩短直至有兄弟。

由可得为的兄弟，则有对应的顶点为兄弟，且这两个顶点在二叉树中的深度都等于树高。

25

证明： 在阶的连通图G中 ，存在至少两个顶点，从G中删除这两个顶点后所得图仍为连通。

由推论2.2可知连通图有生成树，记为。

由定理2.2可知树T至少有两片叶，记为。

从中删去得树显然仍然连通

从G中删去得到图中，易知且存在轨道， 则 仍然连通。