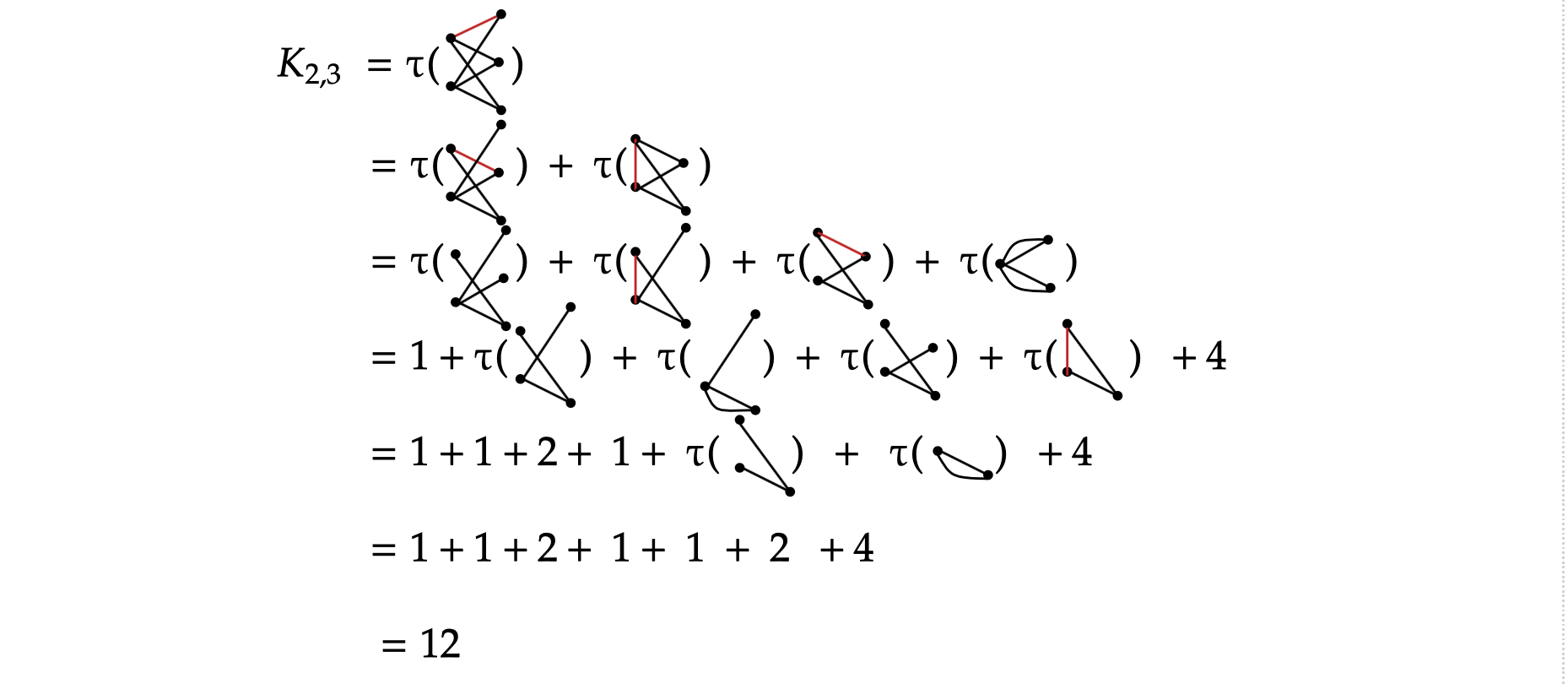
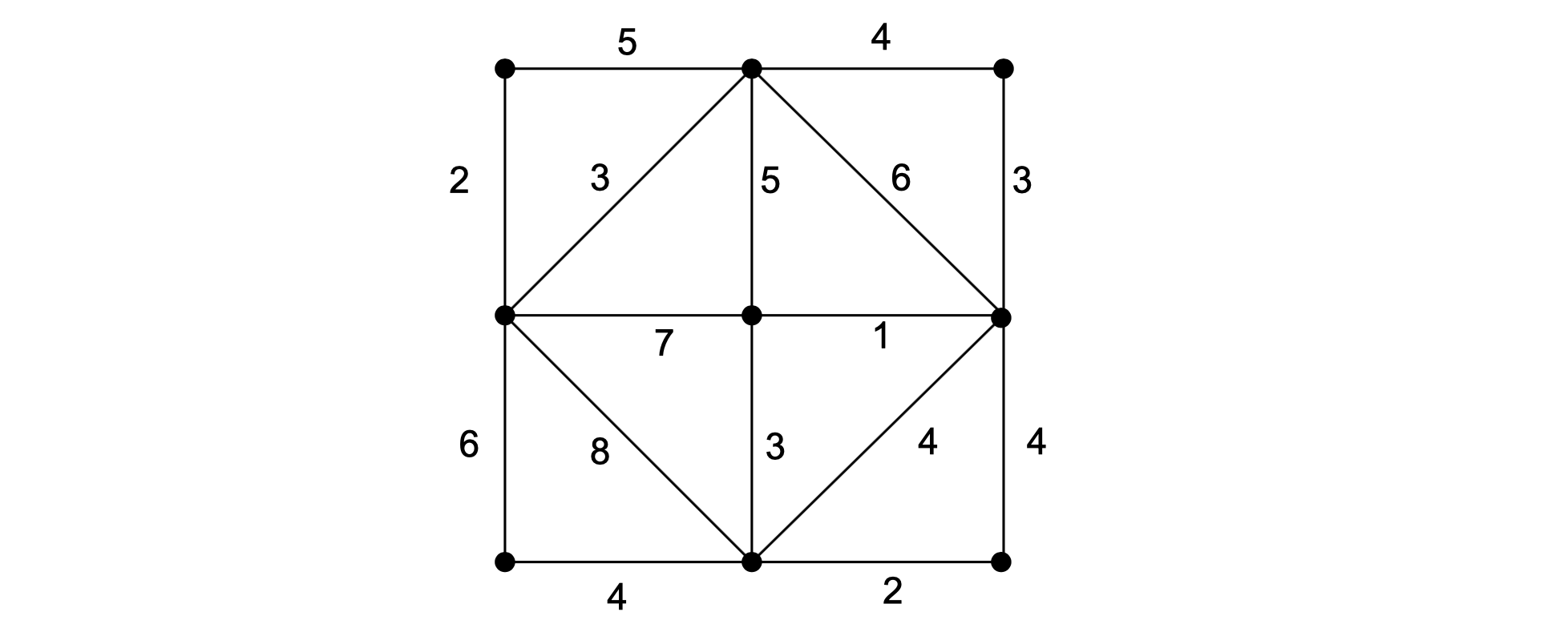
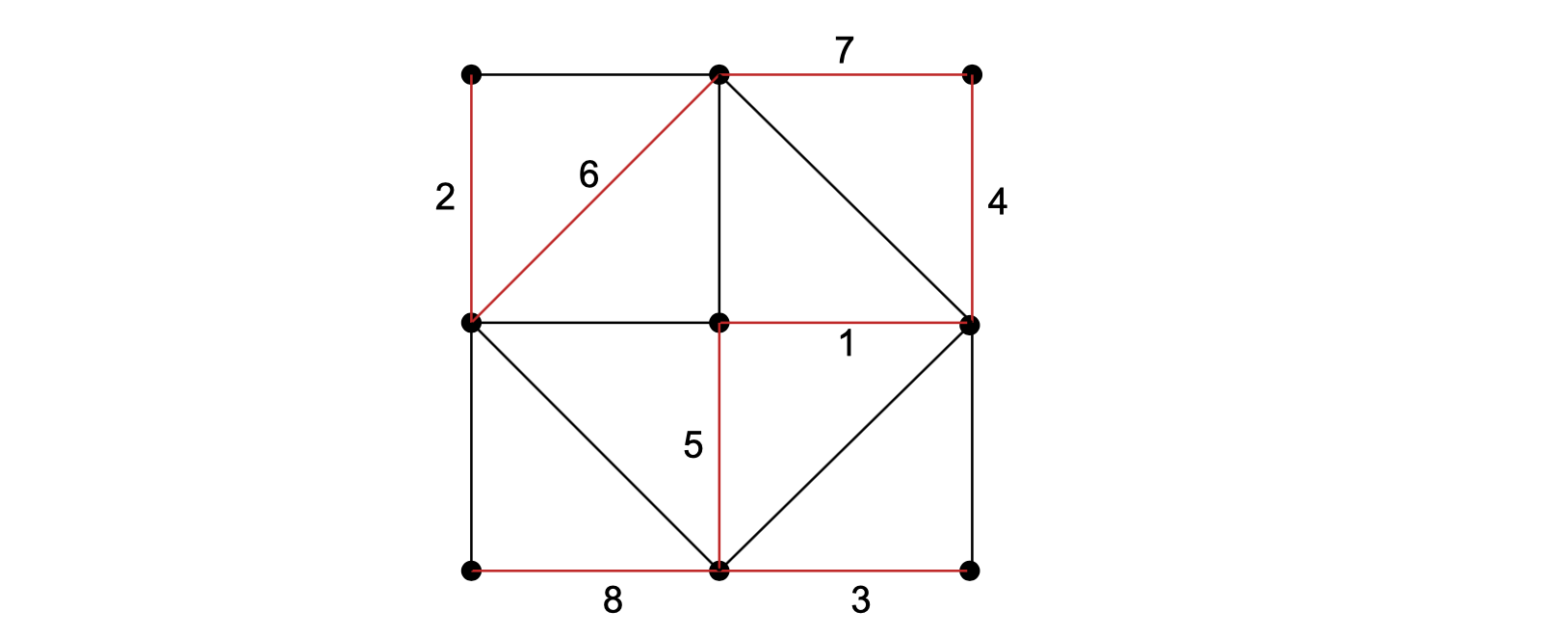
1*
G是简单图,则有
方法1(Euler定理):
因为G是简单图 所以∀v∈V(G),有deg(v)≤v-1
则
由Euler定理,,得证
方法2(组合):
在简单图中,任意两顶点之间最多存在一条边
即
3
画出所有四个顶点不同够的简单图
一共11个(图略)。
4*
任何至少由两个人构成的群体中,其中有两个人,他们的朋友数一样多。
证:将每个人看作顶点,两个人是朋友则在这两人所代表的顶点之间加一条边,因此问题等价于:在对任意满足的图G中,存在,使得.
反证法:假设对任意,都有
deg(v)在G中共有|V(G)|个不同的取值
而deg(v)取值范围为0至|V(G)|-1,恰好有|V(G)|个可能的取值,故每种取值恰好出现一次,分别为0,1,…,
|V(G)|-1
所以存在,使得
即与所有点都不相连,与所有点都相连,矛盾,假设不成立。
得证。
5
人中,每个人至少与其中的n个人认识,则其中至少有4个人,使得这四个人围桌而坐时,每个人旁边都是他认识的人。
该问题等价于证明图中存在长度为4的圈,等价与存在2个人,他们共同认识的人有两个即以上。
用反证法容易证明。
7*
证明下面的结论:
(1)
(2)设G是二分图,
(1)证:不妨设 ,其中|X|=m,|Y|=n
由定义,
则
由Euler定理,
(2)
由(1)可得
所以
即
8
设G是图,给定的非空真子集V‘。记k为一个端点在V’中,另一个端点在中的变数。若V’中度数为奇数的顶点数为偶数,则k为偶数;否则,k为奇数
设是V‘的顶点导出子图的边的个数,则k有:
因为 一定是偶数,所以k的奇偶只和有关:若V’中度数为奇数的顶点数为偶数,则k为偶数;否则,k为奇数。
9
每个顶点的度数都是2的连通图是一个圈。
用最长轨法来证明,设为,显然有可得该图中必有圈,并且连接的必然是 ,否则某个顶点的度数会是3。
10
证明活说明下面的结论:
(1) 若,则称G是自补图。证明:若G是自补图,则。
(2)有多少个的自补图。
由于同构可以得到如下的结果:
则必有:
自补图有2个。
11
构造以一个二分图G,使得G不与任何K维立方体的子图同构。其中,k为任意正整数。
13
任给图G,都满足
由定理得:
又因为:
可得上述证明式子。
14*
我们将图G中所有定点的度数按照从大到小的顺序排列,称为图G的度数序列。证明:
(1) 7,6,5,4,3,3,2 和 6,6,5,4,3,3,1都不是简单图的度数序列。
(2) 设是简单图的度数序列,则是偶数,且对于任意,都有
(1) 证明:从序列可以看出两个图顶点个数均为7
- 若是简单图,则必有,但是存在度数为7的点,则
7,6,5,4,3,3,2不是简单图。
- 若是简单图,则因为只有7个顶点,序列中的两个度数为6的顶点与图中每个点都相邻,则必有,但存在度数为1的 点,则不是简单图。
(2) 证明:由书上定理1.1可得
显然是偶数。
对于第二个证明式,设顶点依次是。
然后我们进行拆分,设,其中:
- 是的顶导出子图 的度数之和。易得 ;
- 是之间连线数。并且 可以给予的的最大的度数之和是:,所以有:
综上可得:
15
任给无环图G,G有一个生成子图H,满足:(1) H是二分图;(2)任给,都有
采用类似“最长轨”的思想,这里假设是边数最多的二分生成子图,并架设命题不成立。
根据假设,里存在点使得,并假设此二分图划分为X和Y,且
16*
假设G是简单图 ,且,则 G中有长为k的轨道。
证明:此题用最长轨法证明,设是该图的最长轨。假设它的长度小于k,即。
对于,因为,除去与轨道上的顶点有连线外, 至少与轨道外的一个顶点的相邻,与最长轨的假设矛盾!
则 G的最长轨长度至少为k,所以存在长为k的 轨道。
19*
(1)证明:任给,都满足
(2)说明:对于图G的任意顶点v,用 替代,(1)中的公示未必成立。
(1)证明:假设e在连通片中,若去掉后仍连通,则有:
若使G1分成了两个连通片,则有:
综上有:
(2)举反例即可:
26*
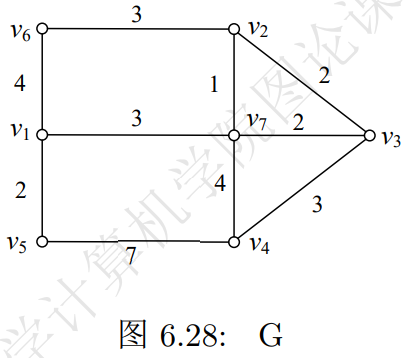
一个公司在六个城市有分公司,下面的恶矩阵号元素是到的机票价格,试为该公司制作一张 到每个城市的路线图,使得每个城市的机票价格都最便宜。
下面用表格来表示迭代
| 迭代次数i |
|
|
|
|
|
S |
| 0 |
50 |
|
40 |
25 |
10 |
|
| 1 |
50 |
|
50 |
25 |
10 |
|
| 2 |
35 |
45 |
35 |
25 |
10 |
|
| 3 |
35 |
45 |
35 |
25 |
10 |
|
| 4 |
35 |
45 |
35 |
25 |
10 |
|
| 5 |
35 |
45 |
35 |
25 |
10 |
|
路径的答案不止一种: